| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- llama
- nlp
- 언어모델
- supervised ml
- Machine Learning
- 머신러닝
- 인공지능
- Andrew Ng
- Regression
- Unsupervised Learning
- bingai
- 챗지피티
- Scikitlearn
- 프롬프트 엔지니어링
- neural network
- learning algorithms
- Supervised Learning
- AI
- 딥러닝
- AI 트렌드
- coursera
- LLM
- feature scaling
- 인공신경망
- Deep Learning
- ML
- GPT
- feature engineering
- ChatGPT
- prompt
- Today
- Total
My Progress
[Advanced Learning Algorithms] Neural Network Training - 2 본문
[Advanced Learning Algorithms] Neural Network Training - 2
ghwangbo 2024. 1. 16. 20:231. Details of training
#Step 1 : Specify how to compute output given x and parameters w, b (define model)
#Math : f_w,b(x) = ?
#Logistic Regression
z = np.dot(w,x) + b
#Step 2 : Specify loss and cost
#Math: L(f_w,b(x), y)
# J(w,b) = 1/m sigma L (f_w,b(x(i)), y[i])
f_x = 1 / (1 + np.exp(-z))
loss = -y * np.log(f_x) - (1 - y) * np.log(1 - f_x)
#Train on data to minimize J(w,b)
w = w - alpha * dj_dw
b = b- alpha * dj_db
If we were to illustrate the code above in neural network, it would be the code below
Code
import tensorflow as tf
from tensorflow.keras.import Sequential
from tensorflow.keras.layers import Dense
model = Sequential([
Dense(units = 25, activation = 'sigmoid')
Dense(units = 15, activation = 'sigmoid')
Dense(units = 1, activation = 'sigmoid')])
from tensorlow.kears.losses import BinaryCrossEntropy
model.compile(loss = BinaryCrossentropy())
#Uses "Back Propagation" to compute derivate
#Gradient descent
model.fit(X, Y, epochs = 100)
Epochs: number of steps in gradient descent
Logistic loss is also known as BinaryCrossEntropy since the output is either 0 or 1.
2. Different Activation functions
2.1 Intro
Linear Activation function
- Often refer as "no activation function"
Logistic Regression Function
- Sigmoid Function for classification
ReLU (Rectified Linear Unit)
- ReLU is also known as Rectified Linear Unit activation function.

The image above shows the ReLU activation function graph. As you can see if z or x is less than 0, y is equal to 0. But is z is greater than equal to 0, y is equal to z.
ReLU is the common choice for the hidden layer.
Why?
- ReLU is much faster than the sigmoid function since it only computes max(0, Z).
- Using Linear Activation function or Sigmoid function for hidden layers will not allow to compute complex features.
- A function from the previous layer, w(x) + b, is an input for the next layer, so the equation will be w(w(x) + b) + b.
- As it goes on and on until the output layer, this will only be equal to linear regression formula.
- If we use sigmoid function in output layer with all linear activation function for the hidden layers, the resulting equation will only be equal to the sigmoid function
Conclusion: Do not use linear activation in hidden layer.
2.2 Choosing activation functions
For output layers
Binary Classification
- Sigmoid
Regression(y <= 0 && y >= 0)
- Linear Acivation function
Regression(y>=0)
- ReLU
For hidden layers
- People often use relu function rather than sigmoid because it is much faster.
- Sigmoid function has 2 areas where the slope goes flat while relu has one.
2.3 Why do we not use linear activation functions
Linear Function of a linear function is a linear function.
If sigmoid function is an output layer, the calculation of the whole neural network layer is just simply a logistic regression.
3. Multiclass Classification
3.1 Intro
Multiclass Classification is a problem with more than two outputs(categories).
For example, we want to compute the genre of a movie. It could be adventure, fantasy, thriller, and etcetera.
Then how do we predict the genre of a movie?
Originally, sigmoid function allowed us to classify to categories, whether the output is 0 or 1.
By using Softmax Regression algorithm, we can solve the problem with more than two outputs.
3.2 Softmax Regression Algorithm
This algorithm is the generalization of logistic regression algorithm to the multiclass classification contexts.
Intuition
Logistic Regression has 2 possible outputs values
z = w * x + b
a1 = g(z) = 1/ 1+ e^z = P(y = 1 | x) -> Probability of x to be 1.
a2 = g(z) = 1/ 1+ e^z = P(y = 0 | x) = 1 - a1 -> Probability of x to be 0.
But Softmax Regression has N outputs.
Lets say there are 4 possible outputs
z1 = w1 * x + b1
z2 = w2 * x + b2
z3 = w3 * x + b3
z4 = w4 * x + b4
Probability of 1 to happen(a1) is a1 / (a1 + a2 + a3 + a4)
Cost functions for Softmax Regression
loss = {- loga1 if y = 1
- loga1 if y = 2
-loga^n if y = N}
If we were to graph the loss, it would be
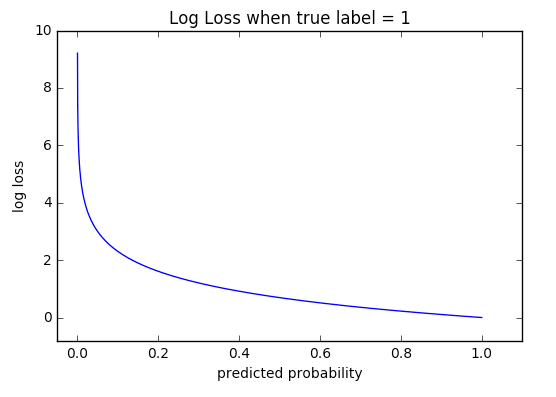
Implementation of Softmax Function
There could be roundoff error depending on the way how you express the function.
If you can fix this issue for logistic function by declaring an extra parameter.
model.compile(loss = BinaryCrossEntropy())
#this version fixes roundoff error
#logit = z
model.compile(loss = BinaryCrossEntropy(from_logits = True))We have to do this by setting output layer a linear activation function.
We can apply the same method to softmax function.
What we are basically doing is we are plugging in a unsolved logistic regression function instead of plugging in a solved probability of n to happen.
3.3 Classification with multiple outputs
Lets say we want to detect and classify multiple objects: car, pedestrian, dog
We can solve this problem by having 3 different softmax function in the output layer.
'AI > ML Specialization' 카테고리의 다른 글
| [Advanced Learning Algorithms] Machine Learning Development Process - 4 (0) | 2024.01.22 |
|---|---|
| [Advanced Learning Algorithms] Diagnostics / Bias & Variance - 3 (0) | 2024.01.16 |
| [Advanced Learning Algorithms] Neural Network - 1 (0) | 2023.08.03 |
| [Supervised ML] Review - 11 (0) | 2023.08.03 |
| [Supervised ML] The problem of overfitting / Regularization - 10 (0) | 2023.08.01 |



